A Markov Chain can be defined as a stochastic model that describes the possibility of events that depends on previous events. A Markov chain gives the probability of transiting from one event to another event. The transition of the variables from one event to the other depends on a mathematical property called Markov Property. Markov property is used in all the Data science programs and its applications. This property is also used by data science beginners, in Data analytics certifications and has gained importance in all the best data science programs online and different courses offered.
To define the process mathematically, it can be expressed as follows:
Markov Chains are generally defined as a process in a continuous-time or definite space
Let a Stochastic process be X= {Xn , n€N } in a definite space say ‘S’ is discrete-time Markov Chain if: For all n ≥ 0, X n € S
For all n ≥ 1, for all i0, i1, ….in-1, in € S , then
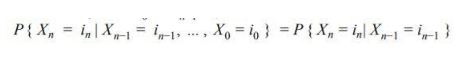
The types of Markov chains are based on the state space of the system and its time index and the different types of Markov processes can be identified by the space and time which is continuous or discrete shown as below:

Discrete Markov Chain
A discrete Markov Chain is the process that has variables in a sequence X1, X2, X3 with a Markov property in which the probability depends on the current or present state to move to the next state but not on the previous states.
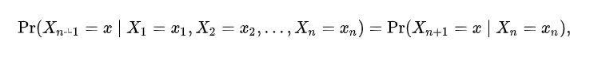
It satisfies the conditional probabilities:
Pr (X1 = x1 , x2 , ….. , Xn = xn ) > 0 in a definite space system.
There are other variations in the discrete Markov chain like Time – Homogeneous chain where the probability is independent of ‘n’. There is other Markov chain with an order of ‘m’ in which the previous states influence the future states.
Continuous-Time Markov chain
The Continuous-Time Markov Chain has a definite space with a defined probability depending on the space system. It is a Transition rate matrix Q with that of the space dimension. The qij elements are should be such that they are non-negative for i≠j and for i=j elements should be such that every row of transition rate matrix should sum to zero.
The Continuous-Time Markov Chain can also be defined as three equivalent processes such as Infinitesimal definition, Jump chain/holding time, Transition probability definition.
Properties of Markov Chains:
Reducibility
Markov chain has Irreducible property if it has the possibility to transit from one state to another. Let’s say a state P has accessibility to the state Q (P-> Q), then the chain has irreducible property if state originated from state Q has Non zero probability to transit to state P. This transition is called Communicating class by state P with state Q. A chain is also said to be as Irreducible if it has a single space communicating class. Suppose if it has zero probability to the transition of state P to Q, then we can say that community class is closed.
Periodicity
If a state P has period R if a return to state P has to occur in R multiple ways. For this state the Period is defined as: R=GCD{n>0: Pr( Xn =P | X0 = P) > 0 }. If the said condition is not satisfied, then there is no period for that state and may not reach to another state.
Transience and recurrence
A Transient state P can be defined as the state where it has Non-Zero probability to never reach its own state P is called as Transience. A state can be said as Recurrent if it is not Transient failing the above-mentioned condition.
Ergodicity
A state is defined as Ergodic if it has a Period of 1 and Recurrent in nature. If a Markov chain has more than one state if one state is non-recurrent or Not periodic then it is Non-Ergodic.
Applications of Markov Chain
There are many applications of Markov chain which are widespread in various range of fields like Physics, Medicine, Biology, Game theory, etc.
Physics
- Markov chains are widely used in many department s of physics for various purposes. It is used in Mechanics and Thermodynamics to find the probabilities of different models used in the system.
- Monte Carlo method is used to find out the Probability distributions for various objects used in experiments.
Biology
- It has wide applications in different domains of Biology. It is used in BioInformatics and Phylogenetics to study the DNA evolution, understanding the genomes.
- It is used to study the population matrix models where the Markov chain is used to understand the dynamics of the population.
- It has wide uses in Neurobiology and Sytems biology to study the models of viruses and the infections caused by it.
Probability Theory
- Markov chains have applications in every use of probabilistic theory like Queueing theory, Game theory, complex programming to solve large and difficult algorithms.
- It is also used to predict the changing trends in customers and their switching behavior with various products and the probability of customers buying that product.
Testing
- Markov chain statistical test (MCST) is a method used to form Markov Blanket which acts as a recursive test model to do exhaustive testing and also in tracking and detections of objects using MCST.
Finance
- Markov chains are used to predict the Bull, Bear and Stagnant markets to estimate the rise or fall of prices and also the credit risk over a period of time.
- It is also used in Economics to predict the rise or fall of the value of an asset determined by a random factor used by the credit rating agencies.
Markov chains are also used in many other areas like Games to predict the moves of the opponent, in music to produce the desired note values, in Social Sciences to figure out different studies using benchmarks or indexes.
Thus, due to Markov chains, demand has raised for the Data Science certifications, courses, and programs online and offline.
Leave a Reply